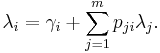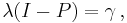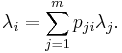Traffic equations

In queueing theory, a discipline within the mathematical theory of probability, traffic equations are equations that describe the mean arrival rate of traffic, allowing the arrival rates at individual nodes to be determined. Mitrani notes "if the network is stable, the traffic equations are valid and can be solved."^[1]

Jackson network

In a Jackson network, the mean arrival rate 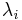$\lambda_i$ at each node i in the network is given by the sum of external and internal arrivals. If external arrivals have rate 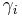$\gamma_i$ and the routing matrix is P, the traffic equations are,^[2] (for i = 1, 2, ..., m)

$\lambda_i = \gamma_i %2B \sum_{j=1}^m p_{ji}\lambda_j.$

This can be written in matrix form as

$\lambda(I-P)=\gamma \, ,$

and there is a unique solution of unknowns 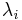$\lambda_i$ to this equation, so the mean arrival rates at each of the nodes can be determined given knowledge of the external arrival rates 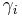$\gamma_i$ and the matrix P. The matrix I − P is surely non-singular as otherwise in the long run the network would become empty.^[1]

Gordon–Newell network

In a Gordon–Newell network there are no external arrivals, so the traffic equations take the form (for i = 1, 2, ..., m)

$\lambda_i = \sum_{j=1}^m p_{ji} \lambda_j.$

Notes

^ ^a ^b Mitrani, Isi (1998). Probabilistic modelling. Cambridge University Press. ISBN 0521585309.
^ Harrison, Peter G.; Patel, Naresh M. (1992). Performance Modelling of Communication Networks and Computer Architectures. Addison-Wesley. ISBN 0201544199.